昨天介紹完單層感知機模型程式,今天要來研究淺層神經網路:
單層感知機模型是只有一個輸入層和輸出層,如果用來做簡單多元線性回歸效果還可以,但是一旦今天是複雜的非線性預測,或是多元分類問題,
單層感知機模型可能就無法解決-->所以我們可能要增加神經網路的層數,今天要來實做就是BP(反向傳播)神經網路,他是由一個輸入層,一個輸出層和多個隱藏層所組成,結構如下: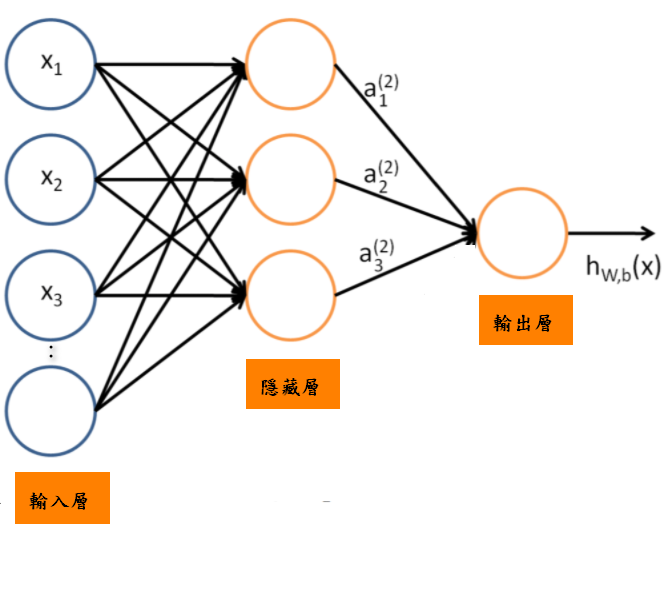

今天用的BF,我打算使用三層網路(一層輸入層,一層輸出層,一層隱藏層)
-->先不要用太多隱藏層(除非可能結果很差)

而BF神經網路概念是:資料先經過輸入-->隱藏-->輸出(正向傳播),在經由估計值和實際值誤差-->回傳給隱藏層並將誤差分散給各層神經元,這樣就可以獲得各個神經元誤差-->就可以修正神經元權重,持續不斷調整,直到估計值和實際值誤差小於一個值或達到最大迭帶上限

所以演算法如下:

(資料來源:維基百科)

基本上,和這個一樣: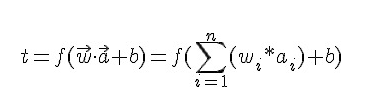

只是多了一個f作為隱藏層的輸出,接下來依照誤差公式:

我們可以對權重去做偏微:

所以到最後權重變化會變成: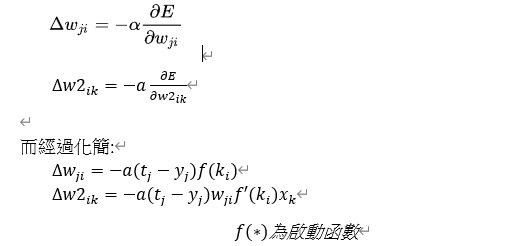

(詳細過程可以參考這篇:https://zh.wikipedia.org/wiki/反向传播算法)
至於關於神經元個數,這邊採用這個經驗公式:

所以知道這個後,明天開始實際來操作時,會找實際的啟動函數來作為例子
依樣先匯入資料,就用昨天的資料並做分割,程式如下:

data=pd.DataFrame([[7,560,5.1,16.68],
				   [3,220,4.9,11.50],
				   	[4,80,4.6,14.88],
				   	[7,330,6.7,18.11],
				   	[16,688,5.2,40.33],
				   	[4,225,5.5,13.50],
				   	[3,340,4.7,12.03],
				   	[10,776,5.1,29.00],
				   	[5,605,6.3,21.50],
				   	[6,150,5,13.75]
				   	],columns=['x1','x2','x3','y'])
print(data)
x=data.loc[:,['x1','x2','x3']]
y=data['y']

#個別標準化處理
x['x1']=(x['x1']-np.mean(x['x1']))/np.std(x['x1'])
x['x2']=(x['x2']-np.mean(x['x2']))/np.std(x['x2'])
x['x3']=(x['x3']-np.mean(x['x3']))/np.std(x['x3'])

print(x)


#新增截距項系數1
x['b0']=1
print(x)

#取前6筆當train
x_train=x.loc[:5]
#取後4筆當test
x_test=x.loc[6:]
print(x_train)
print(x_test)

y_train=y.loc[:5]
y_test=y.loc[6:]

print(y_train)
print(y_test)

好,今天淺層網路神經演算法算是完成,明天就來研究淺層網路神經程式

三個人看著牆上文字,瞬間沉思了起來,之後又互相看來看去,卻像是誰都不知道這是甚麼意思,這時眾人突然感覺空氣開始變冷,牆壁角落開始有冰出現而且慢慢的往三人方向延伸,形成包圍之勢,眼看情勢不對,男子立刻從手中伸出團火焰想阻止冰擴散,而這時娃娃像是領悟到甚麼,突然升起雙手把兩人彈飛到冰上,狐狸一臉驚訝看著娃娃,而男子一臉憤怒看著娃娃,而下一瞬間兩人都被冰凍了起來,一動也不動,同時冰停止蔓延,並且牆壁開始碎裂,最終冰和牆壁還有木棉花都消散在空氣中,只留下娃娃和被凍住狐狸和男子
           --|未來是孤獨,只留我一人追尋|--  MC.SM